Building a Write-Optimized Database Engine: Sorted String Tables (Part 3)

We develop an on-disk representation of data to ensure efficient reads and writes. We also explore auxiliary structures that help us work with such representations better.

In our previous discussion, we focused on managing data within the memory of our log-structured database. We were able to handle data operations like writing, updating, and reading efficiently using well-known structures like trees or skip lists. If you are not fully caught up on those details, I suggest looking back at the previous issue.

Building a Write-Optimized Database Engine: The Memtable (Part 2)

However, keeping the data only in memory is not enough, primary storage is volatile and is not reliable for long-term storage of data in our database. Therefore, we need to find a way to store our data on the disk, beyond just keeping it in memory.

1. We’ll understand the access patterns we want to support for our data.

2. We’ll develop on-disk representations to support those access patterns.

3. We’ll add support for all the major APIs to the on-disk structures such as Get and RangeScan.

Sorted String Tables

We already discussed the basics of Sorted String Tables in the introductory issue of this series.

The data within the memtable remains in memory until a specific flush condition is triggered, usually when the size of the memtable reaches a predetermined threshold. At this point, the contents of the memtable are sequentially flushed to the disk, creating an immutable file known as an SSTable (Sorted String Table). The name Sorted String Table comes from the fact that the data is written to the disk in sorted order (same as the memtable). Since the data is written in sorted order on this disk, the system can make use of a simple binary search algorithm to look up entries.

Building a Write-Optimized Database Engine: High Level Architecture (Part 1)

SSTables, being immutable, primarily serve read requests and must offer efficient data access. The sorted data helps with this, but additional mechanisms are necessary for optimal performance. Given that SSTables reside on disk and entries vary in size, directly calculating offsets for performing a binary search over the keys is not possible without first reading all the data. This approach is impractical due to the high disk I/O costs and the impracticality of loading entire SSTables into memory, especially for files spanning multiple gigabytes.

Indexes

An important optimization for addressing this challenge is the incorporation of an index. Positioned at the SSTable's beginning, this index acts as a directory, listing keys in sorted order alongside their corresponding offsets within the file. The index is much smaller in size as compared to the actual SSTable data and is often kept loaded into the LSM Tree’s memory, enabling efficient binary searches to locate entries. Once the desired entry’s key is identified in the index, the system can directly access its offset in the SSTable file to read the data, significantly reducing access times.

SSTable with an index in the beginning. The index contains keys present in the SSTable in sorted order along with their offsets in the SST file.

Sparse Index

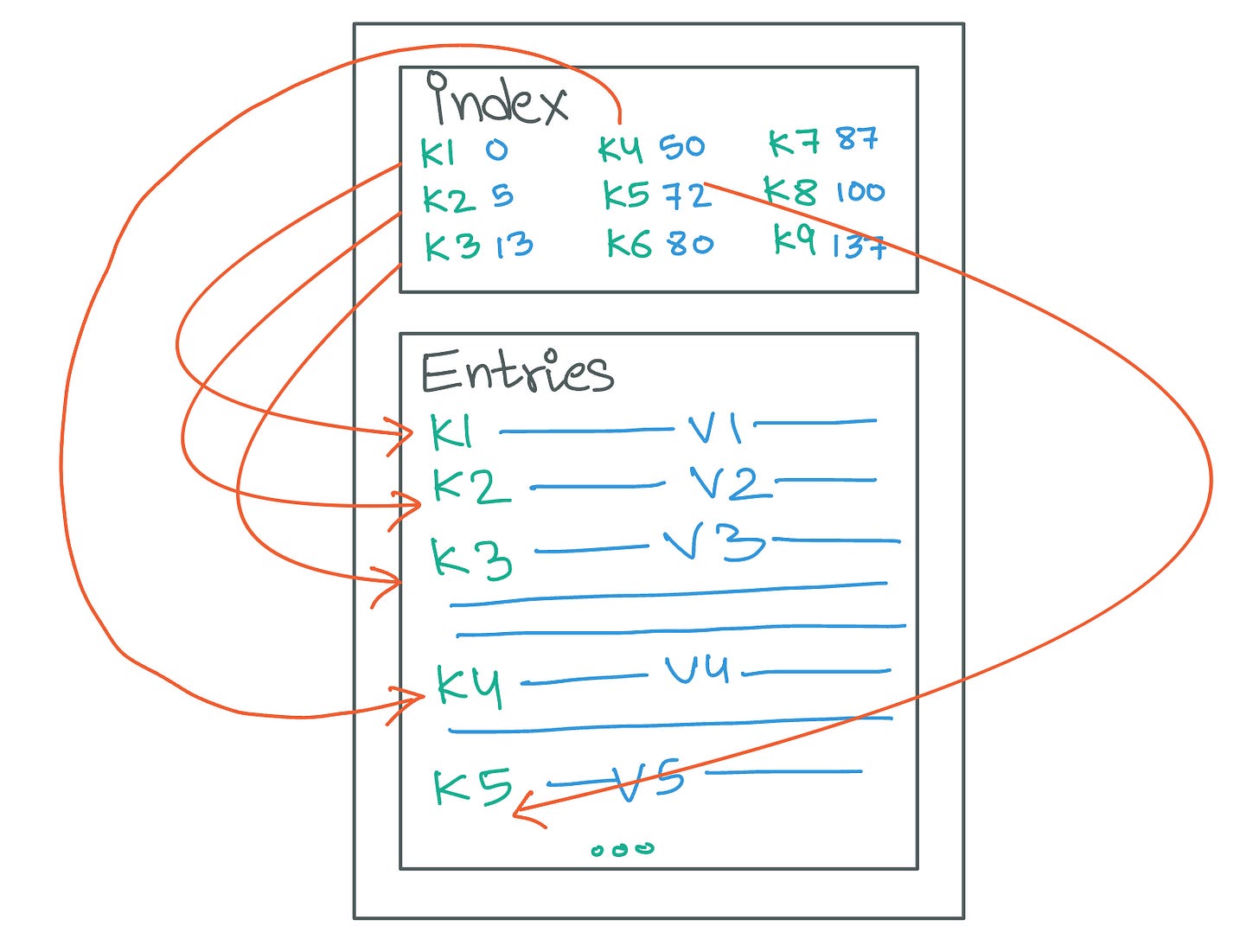
In scenarios where SSTables grow exceptionally large, the corresponding full indexes can also become sizable, potentially impacting system performance due to the increased memory requirements. To mitigate this, databases may implement sparse indexing, a technique that reduces index size by including only a subset of the keys present in the SSTable.

Using a sparse index means that not every key in the SSTable is directly referenced in the index. For example, in an SSTable containing keys 'A', 'B', 'C', 'D', and 'E', a sparse index might only list 'A', 'C', and 'E' along with their offsets. This approach assumes that keys not explicitly indexed, such as 'B', reside between the indexed keys 'A' and 'C'. When a request for 'B' is made, the database system leverages the sparse index to narrow down the search to the segment between 'A' and 'C' on the disk, thereby reducing the search space compared to scanning the entire table.

Sparse indexing effectively balances memory usage with access speed. While it may slightly increase the time required to locate non-indexed keys due to the need for additional disk reads within the identified segments, this compromise is often acceptable given the significant reduction in memory footprint. Moreover, this strategy aligns with the LSM tree's design philosophy of optimizing write efficiency while maintaining reasonable read performance.

Bloom Filters

We previously discussed that reads in an LSM tree involve progressing through various data structures - starting from the most recent memtables and moving through SSTables in descending order of their creation—to locate the requested key.

While this search strategy is effective for maintaining data consistency and integrity, it introduces a significant performance bottleneck for non-existent key lookups. Specifically, the need to perform binary searches across each SSTable's index for a key that ultimately isn't present becomes exceedingly time-consuming, leading to increased latencies. This problem is amplified in the case of sparse indexes since one needs to perform disk IO for non-indexed keys (and non-existent keys will always be non-indexed).

To effectively address this challenge LSM tree-based databases employ a probabilistic data structure known as a Bloom filter for each SSTable. A Bloom filter provides a fast means of assessing whether an element is likely not part of a set - ideal for quickly determining the absence of a key in an SSTable without resorting to disk reads. They achieve this by allowing a small probability of false positives (where it might incorrectly indicate that an element is in the set when it is not), which is a trade-off for their ability to provide immediate feedback on the non-existence of a key without accessing the disk.

A bloom filter involves three primary components: an array of bits, several hash functions, and the elements to be added or checked against the filter. Here's a step-by-step explanation of how a Bloom filter operates:

1. Initialization: Start with a bit array of m bits, all set to 0, and k different hash functions, each capable of hashing an input to one of the m bit positions in the array. Bloom filters often make use of an algorithm called Murmur Hash.¹

2. Adding Elements: To add an element to the set, the element is hashed by each of the k hash functions. Each hash function will produce an index to a bit in the array. All bits at these k indices are set to 1. If a bit is already set to 1, it remains 1.

3. Querying Elements: To check if an element is in the set, the same k hash functions are applied to the element. This generates k indices. If any of the bits at these indices is 0, the element is definitely not in the set (no false negatives). If all bits at these indices are 1, the element might be in the set (but could be a false positive).

4. False Positives: The chance of a false positive increases with the number of elements added to the set because more bits in the array become set to 1. The probability of false positives can be reduced by increasing the size of the bit array m and the number of hash functions k, but this also increases the space and computational overhead.

Our Bloom Filter implementation uses 3 hash functions

Integrating Bloom Filters in the Read Path

When a read request is issued, the system first consults the Bloom filter associated with each SSTable in sequence. If the Bloom filter indicates that the key is not present, the database can skip the binary search on its index and also any potential disk I/O for that SSTable and move on to the next one. This significantly reduces the amount of disk I/O required for read operations, especially for non-existent keys.

Bloom filters, by design, may allow a small probability of false positives (where a key appears to be present but is not). Still, crucially, they do not produce false negatives (where a key is present but appears not to be). This ensures that while some unnecessary searches may occur due to false positives, the database will never overlook an existing key.

Implementing the SSTable

The complete code we are working towards is available at github.com/JyotinderSingh/goLSM

While an SSTable primarily resides on disk, managing it effectively requires a corresponding in-memory representation. For each SSTable, we maintain some critical metadata in memory, including its bloom filter, index, file handle, and an auxiliary field known as dataOffset. This setup facilitates efficient access to SSTable data:

The bloom filter and index are defined using protobuf, offering a structured and efficient way to serialize and deserialize these components. The protobuf message definitions for these components are pretty straightforward.

The dataOffset field in the SSTable struct plays a crucial role by marking the starting point of the actual data entries within the SSTable file. This offset accounts for the bytes consumed by the bloom filter, index, and any other metadata that may be stored ahead of the data entries. By maintaining this offset in memory, we streamline navigating to and reading the data entries from the on-disk file.

Writing the SSTable to the Disk

Upon reaching its maximum size, a Memtable must be flushed to disk to ensure data durability. The Memtable's GetEntries() API allows the system to retrieve all entries it contains in sorted order. Using these entries, the system constructs a bloom filter and an index, both essential for efficient data retrieval and minimizing disk I/O operations during future queries to the SSTable.

The SerializeToSSTable() method uses the buildMetadataAndEntriesBuffer() utility to build the bloom filter and index and load the memtable entries into a buffer.

The mustMarshal() and mustUnmarshal() methods are utility wrappers around the Protobuf marshaling and unmarshalling methods. Rather than returning errors, they induce a panic if marshaling or unmarshalling fails. The rationale behind this approach is straightforward - any failure in these operations is indicative of a severe corruption within the database system, and we would not want to serve any further requests.

Finally, all this information is fed into the writeSSTable() method which persists this data to the disk in the form of an SSTable and returns the associated dataOffset.

The SerializeToSSTable() method returns an SSTable object, which contains the SSTable file handle along with related metadata to efficiently read entries from it.

Opening an SSTable

For reconstructing an SSTable's in-memory representation from disk upon a system restart or when needed, we make use of the OpenSSTable() method. This method reads the metadata of an existing SSTable from its disk file and loads it into memory, without loading the actual data entries. This metadata includes the bloom filter, index, and the offset where the data entries begin (dataOffset).

Read APIs

Get

To serve a read request from an SSTable, the system first consults the SSTable's bloom filter with the requested key. If the bloom filter returns a negative result, this indicates that the key is definitely not present in the SSTable, allowing the system to immediately return nil to the caller, thereby avoiding unnecessary disk I/O.

If the bloom filter suggests the possible presence of the key, the next step is to consult the SSTable's index (by performing a binary search on it). The index, which maps keys to their offsets within the SSTable file, is used to find the exact position of the key's corresponding data entry in the SSTable file. If the index confirms the key's presence by providing an offset, the system then calculates the actual position to seek in the file by adding the dataOffset (which marks the start of the data section in the SSTable file) to the key's offset obtained from the index.

Finally, the system seeks to the calculated position in the SSTable file and reads the data entry. This entry is then returned to the caller.

RangeScan

To conduct a range scan operation within an SSTable, the process begins by identifying the offset for the smallest key that is greater than or equal to the startKey. Since the data within the SSTable is stored in a sorted manner, knowing this offset allows us to efficiently locate the starting point of the range.

Once the starting offset is determined, the system begins reading entries from the file, starting from this offset plus the dataOffset (which accounts for the metadata at the beginning of the SSTable file). It continues to read sequentially until an entry is encountered with a key larger than the endKey.

SSTable Iterator

In upcoming discussions, we will explore a tiered compaction strategy for managing our on-disk SSTables. Compaction is a critical maintenance operation that merges multiple SSTables into a single, consolidated table. This process is essential for reducing read and write amplification, thereby enhancing the overall efficiency of the storage system. A straightforward approach to compaction might involve loading the entirety of the SSTable data into memory to perform the merge. However, this method quickly becomes impractical as the size of compacted SSTables can reach several gigabytes, making it infeasible to hold all of this data in memory simultaneously.

To address this challenge, we will develop an SSTable iterator. This iterator functions similarly to container iterators found in various programming languages, enabling iteration over the contents of an SSTable while only loading the current entry into memory. Such an approach allows for the efficient traversal of large SSTables without the risk of running out of memory. By leveraging an iterator, we can perform compaction operations in a memory-efficient manner, iterating through entries of multiple SSTables sequentially and merging them into a new SSTable without necessitating the load of entire tables into memory.

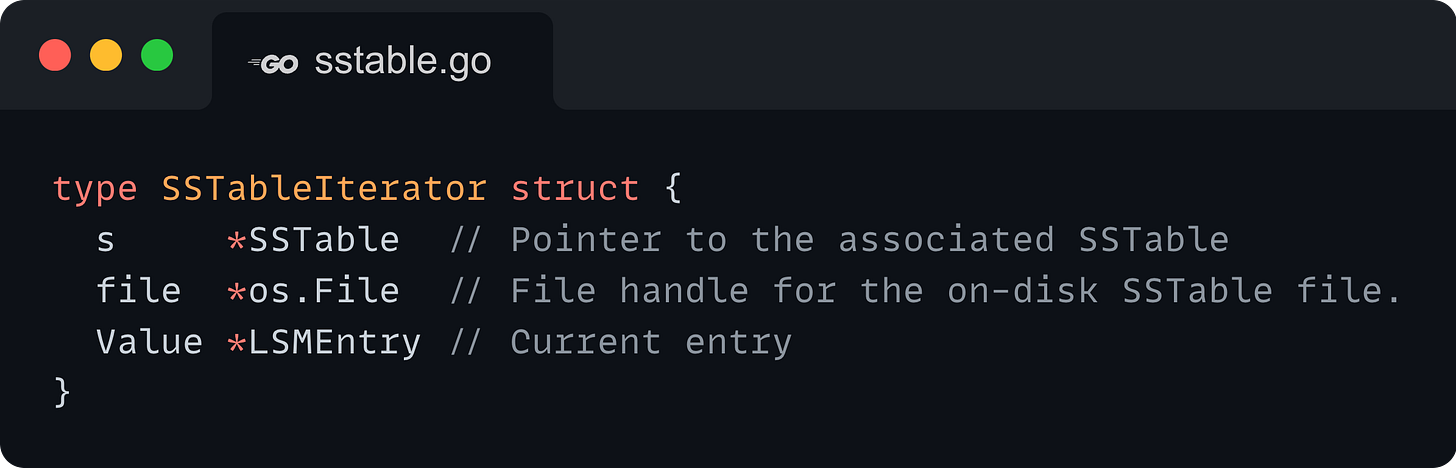
The SSTableIterator struct contains three fields:

1. A pointer to the in-memory SSTable representation.

2. The file handle to the on-disk SSTable file.

3. The current value that is being pointed to.

Instantiating an SSTableIterator

The SSTable struct provides a Front() method that returns an SSTableIterator pointing to the first element of the SSTable.

The Front() method first opens a new file handle to the SSTable file for reading. It then seeks to the start of the entries in the SSTable using the dataOffset and reads the first entry. We set the newly created file handle and the entry on the SSTableIterator instance and return it to the caller.

Iteration

The SSTableIterator includes a Next() method, which allows sequential traversal of entries within the SSTable. The method's implementation is straightforward: it reads the subsequent entry from the SSTable and updates the iterator object with this new entry.

If an error occurs during the reading process, the method first checks if the error corresponds to an EOF condition, signifying the end of the SSTable. This scenario is expected. However, if the error is not an EOF, indicating an unexpected issue, the system triggers a panic. This response is by design, as any error other than EOF during iteration likely points to corruption within the SSTable file. In such situations, we want to exit and not receive further requests.

Coming up

In this issue, we designed and implemented an efficient and high-performance Sorted String Table. We understood the access patterns and accordingly implemented optimizations such as bloom filters and indexes. We also developed an SSTableIterator enabling efficient iteration over SSTable entries without the overhead of loading the entire dataset into memory. This will be particularly crucial for developing a memory-efficient compaction mechanism.

Having established the foundational components of the LSM Tree, including both in-memory structures and on-disk SSTables, we are now ready to integrate these elements into a comprehensive LSM Tree implementation. The upcoming issues will focus on developing the primary interface of our log-structured database engine. This interface will leverage both the in-memory and on-disk components to achieve exceptionally fast and reliable data writes. Moreover, we will explore strategies for crash recovery and maintenance operations, such as compaction, to ensure the database's durability and performance consistency.

References

1. Designing Data Intensive Applications - Martin Kleppmann

2. Database Internals - Alex Petrov

1. https://x.com/arpit_bhayani/status/1748544533145808931